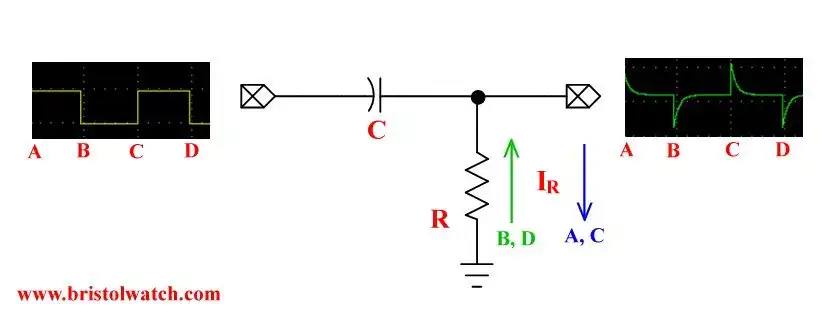
Fig. 1 Basic differentiator RC circuit.

Introduction to RC Differentiator Circuits and Uses

by Lewis Loflin

This is a tutorial on RC differentiator circuit operation. This is simply an RC timing circuit where the capacitor is on the input and the output is taken from the resistor.

I am assuming a 50% duty cycle square wave for input.

Fig. 1 illustrates the circuit in question. A square wave goes HIGH a rush of current (blue) to C through R creates a positive going spike. When C is fully charged the output voltage goes to zero.

When the input square wave goes LOW a rush of current in the opposite direction creating a negative going spike. This also goes back to zero when C fully discharges.

This charge or discharge curve is T = R * C - 5T is fully charged or discharged. If 5T is less than half the period (1/f) of the input C will fully charge-discharge. If 5T is greater than half the period, C will neither fully charge or discharge fully before the next change in logic voltage level.

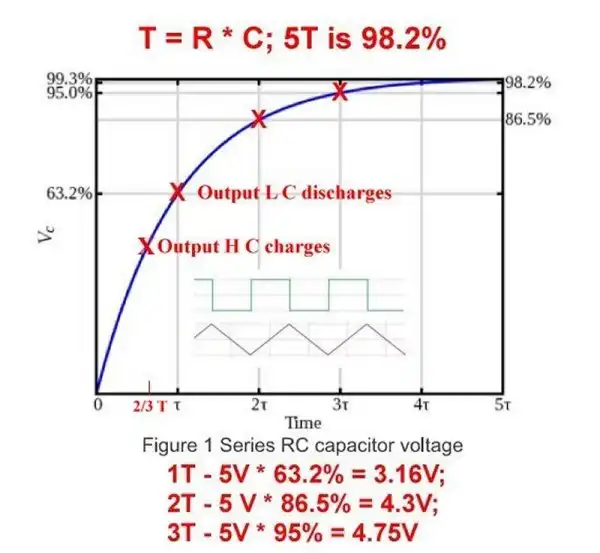
Fig. 2 Capacitor charge curve.

Fig. 2 illustrates a RC charge curve.

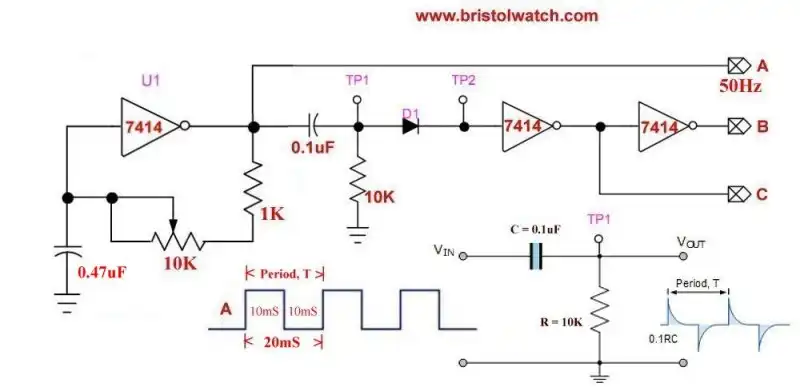
Fig. 3 SN7414 square wave generator and differentiator circuit.

Fig. 3 illustrates the use of a SN7414 square wave generator using a differentiator circuit to create narrow output pulses at points B and C.

Diode D1 is used to block the negative going pules to TP2.

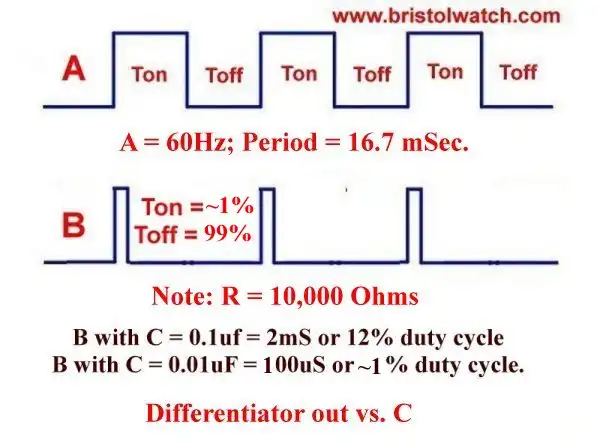
Fig. 4 Differentiator duty cycle versus RC value.

In Fig. 4 we observes the output waveform at point B versus the input to the differentiator circuit. The output pulse width and duty cycle is directly related to the value of C and a 10,000 Ohm resistor.

A value of C = 0.1uF produced a 12% duty cycle of 2 milliseconds.

A value of C = 0.01uF produces a very narrow pulse of 200 microseconds.

See Figures 5 and 6 below.

Fig. 5 A 2 millisecond pulse waveform at 12% duty cycle waveform.

200 microsecond pulse waveform at 2% duty cycle waveform.
Fig. 6 A 200 microsecond pulse at 2% duty cycle waveform.

The next 4 slides (7 through 10) illustrate the effect of increasing input frequency while C is fixed at 0.1uF and R = 10,000 Ohms. The slides are self explanatory. As the frequency increases C can neither fully charge or discharge. The output is a distorted square wave.

In Fig. 11 C was changed from 0.1uF to 0.01uF and even at 480 Hertz produced clean output spikes.

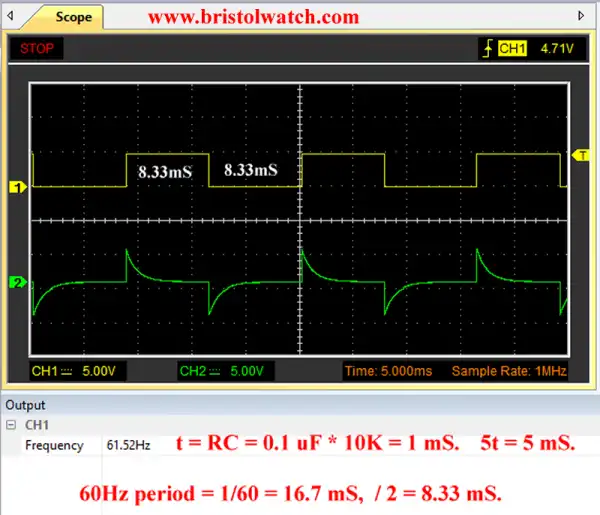
RC differentiator circuit waveform f = 60Hz C = 0.1uF.
Fig. 7 RC differentiator circuit f = 60Hz C = 0.1uF.

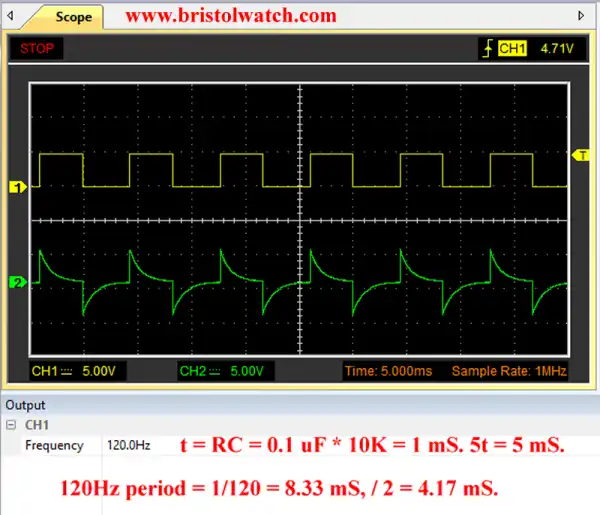
Fig. 8 RC differentiator circuit waveform f = 120Hz C = 0.1uF.

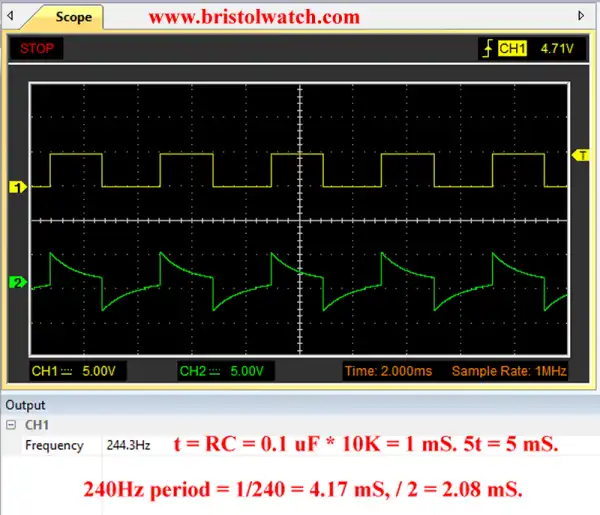
Fig. 9 RC differentiator circuit waveform f = 240Hz C = 0.1uF.

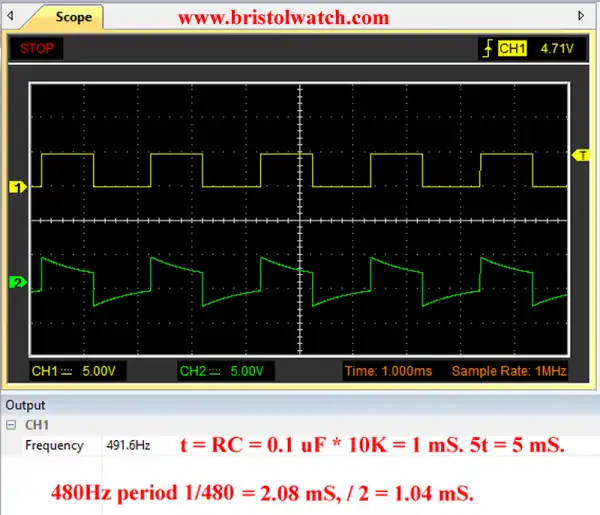
Fig. 10 RC differentiator circuit waveform f = 480Hz C = 0.1uF.

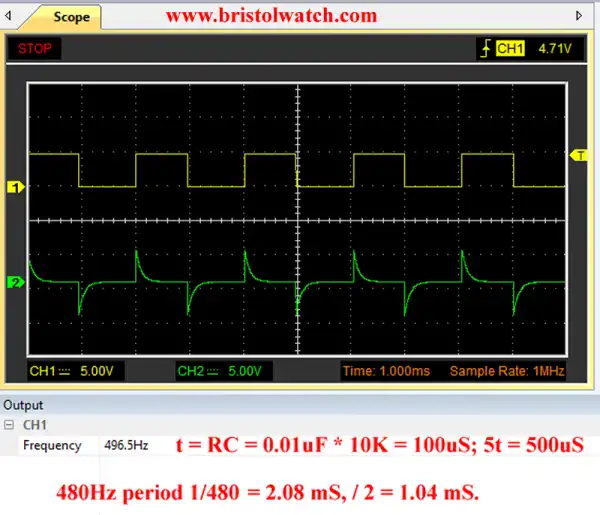
Fig. 11 RC differentiator circuit waveform f = 480Hz C = 0.01uF.

Arduino